Classification of numbers

How are numbers classified?

There are countless ways that numbers can be classified. The classification most commonly used in high school classifies numbers as natural (or counting) numbers, integers, rational numbers, irrational numbers, real numbers and complex numbers.

Why are these sets important to mathematicians?

Many mathematical objects work only with certain types of numbers. For example, polynomials require integer coefficients.

Many mathematical objects are defined using one type of numbers and then expanded to use other types of numbers. For example, x³ = x·x·x, and this can easily be expanded to define integer exponents. But noninteger exponents must be defined a different way. Rational exponents can be thought of as a combination of raising a number to an integer power and then finding an integer root. But irrational exponents must be treated differently.

The idea of different sizes of infinity comes from the difference between countably infinite sets such as the integers and the uncountably infinite sets such as the real numbers.

These sets of numbers often arise because of the need to expand the numbers to have closure under a certain operation. For example, the natural numbers are not closed under subtraction, integers are not closed under division, rational numbers are not closed under finding roots.

The study of Diophantine equations looks for only integer solutions to equations with integer coefficients. For example, Fermat’s last theorem states that, for the equation xⁿ+yⁿ=zⁿ, there are no integer values of x, y, and z if n is an integer greater than 2.

Equations with rational numbers can often be converted into equations with integers, which are easier to deal with. Equations with irrational numbers often cannot be converted into equations with integers.

Computers can specify exact values of rational numbers but only approximations of irrational numbers.

Almost all numbers are irrational.

Why is it important to teach about this classification of numbers?

This classification is often used to practice the ideas of sets, subsets, infinite sets, etc.

This classification can be used to discuss the idea of closure of an operation which in turn is one of the motivations for developing complex numbers.

Many definitions of mathematical objects apply only to numbers belonging to certain sets. For example, the definition of a polynomial requires positive integer exponents.

Many mathematical definitions and theorems are written in set notation which often includes the symbols for these sets.

What is important to know about the classification of numbers?

Students should understand the defining characteristics of:

• Natural numbers (also known as counting numbers)
• Whole numbers
• Integers
• Rational numbers
• Irrational numbers
• Real numbers
• Imaginary numbers
• Complex numbers

Students should know the symbols for the different sets:

• ℕ – natural numbers
• ℤ – integers (also ℤ⁺ – positive integers and ℤ^– – negative integers)
• ℚ – rational numbers
• ℚ’ – irrational numbers (written as the complement of the rational numbers)
• ℝ – real numbers
• ℂ – complex numbers

Students should understand:

• the square root of any integer is irrational unless the integer is a perfect square
• any rational number can be written as the ratio of 2 integers
• any rational number either terminates or ends with a repeating decimal (4/3 = 1.3333…)
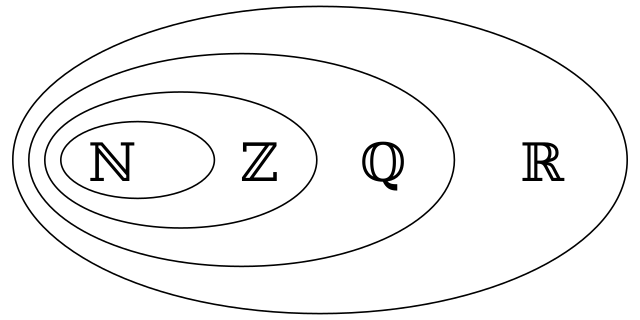
• the relationships between the sets, particularly ℕ⊂ℤ⊂ℚ⊂ℝ⊂ℂ and ℚ⋃ℚ’ = ℝ

Teaching hints:

• “Irrational”, “rational”, and “ratio” are all related. “Irrational” actually came first, because ancient mathematicians did not like the idea of irrational numbers. “Ratio” actually comes from “rational” rather than the other way around. Nevertheless, it is helpful to associate the term “rational numbers” with numbers that are the ratio of two integers.
• “Integer” comes from the Latin meaning “whole” or “untouched” and shares the same root with the words “entire” and “integrity”.
• It is important when introducing the idea of “imaginary” numbers that students understand that imaginary numbers are just as “real” as real numbers. Particularly, the idea of infinity and irrational numbers could also be considered imaginary. Gauss, the famous mathematician, preferred to call them “lateral” numbers.
• It can be said that rational numbers either terminate or end with a repeating decimal. If these two criteria seem unrelated, you can point out that terminating is equivalent to ending with repeating zeros. (3/8 = 0.375000…)

More advanced topics

Closure

Complex numbers

Non-transferable skills:

An algebraic number is a number that is the root of a polynomial with integer coefficients. This term is almost never used in high school. However, the idea may come up because transcendental numbers are numbers that are not algebraic numbers. The very important numbers π and e are transcendental numbers and therefore, the idea of transcendental numbers occasionally comes up. This is not a concept that is applicable outside of abstract mathematics.

Related topics

• Complex numbers
• Closure
• Infinity
• Sets
• Set notation