Set notation

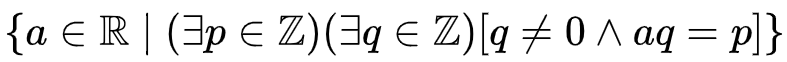
What is set notation?

Set notation is the group of symbols used to describe sets and the relationships between them.

Why is set notation important for mathematicians?

Set theory is the foundation of mathematics and all branches of mathematics have ideas that can be expressed in set notation, although some branches use it more than others. Set notation is commonly seen in algebra, abstract algebra, calculus, geometry, etc.

Why is it important to teach set notation?

Set notation is frequently used throughout algebra I and algebra II to define functions.

Set notation is frequently used in the statements of theorems and in their derivations.

Basic set notation such as {}, ∅, ⊂, ⋃, ∈, etc., may occasionally be encountered in other sciences in high school and more commonly in college STEM courses.

A form of set notation is used in some programming languages, such as Python, which is a common language which often will have a line of code such as: x = [2*y for all y in range(0,10)].

Unions are related to logical ORs and Intersections are related to logical ANDs.

What is it important for the student to understand?

There are several ways that the elements of a set can be described:

• Listing them out (called “enumeration”): A = {1,2,3}
• Giving a pattern (especially for infinite sets): A = {2,4,6,…}
• Describing the set in words (“semantic representation”): {people over 50 years old}
• Defined by a rule that is true for elements of the set and false for elements not in the set (“a predicate”): {x|x>0}

These are the main symbols and notations that a student should understand:

• {}
• A,B,C – sets are often named with capital letters
• {x} – set containing x
• | – such that
• … – and so on
• ∈ – element (or member) of
• ∉ – not an element of
• ⋃ – union
• ⋂ – intersection
• ∅ – empty set
• ℕ, ℤ, ℚ, ℝ, ℂ – natural numbers, integers, rational numbers, real numbers, complex numbers
• A’ – complement of A
• (0,1) – open interval
• [0,1] – closed interval
• ∀ – for all
• ∃ – there exists
• ⊂- subset
• ⊃ – superset

Teaching hints:

• It is important that students are fluent in these symbols because fluency will impact how easily future concepts are grasped.
• ℤ come from the German words “Zahlen”, meaning “number”.
• ℚ come from the word “quotient”, since rational numbers are defined as the quotient of two integers.
• The word “integer” comes from the Latin, meaning “whole” or “untouched” and shares a common root with words such as “entire” and “integrity”.
• ⋃ reminds one of the “u” in “union”, and ⋂ is the opposite of this.
• ⊂ and ⊃ are analogous to < and >, respectively, in that the open end is toward the larger object.
• The style of writing ℕ, ℤ, ℚ, ℝ, and ℂ is called “chalkboard bold”, and can be handwritten with as a normal capital letter with an extra line, either along the left-hand side or along the diagonal.

More advanced topics

These are symbols that may be beneficial for more advanced students:

• |A| – the size of set A
• ℝ×ℝ – the set of all pairs of real numbers, such as the points in a plane
• ℝ²,ℝ³ – similar to above, these refer to the sets of all points in 2 and 3 dimensions, respectively

Non-transferable skills

There are symbols are not typically used outside of advanced mathematics, although they may be encountered in high school mathematics:

• ℵ – cardinality of an infinite set

Related topics

• Closed and open sets
• Sets
• Logic notation