CoMo Science

Spirographs

—

in
  1. What is a spirograph?
  2. The equation of a spirograph
  3. Special situations
  4. Patterns
  5. Website
  6. Desmos
  7. Other curves
  8. Coming up…

What is a spirograph?

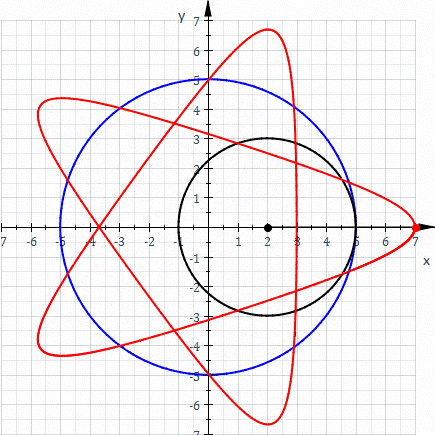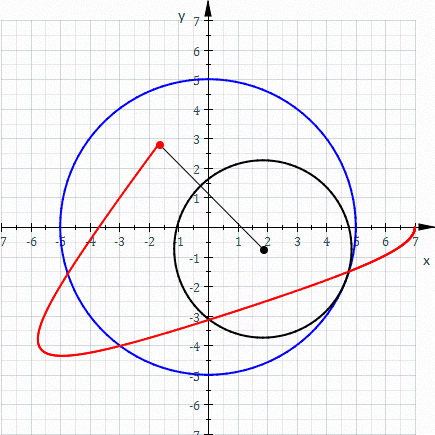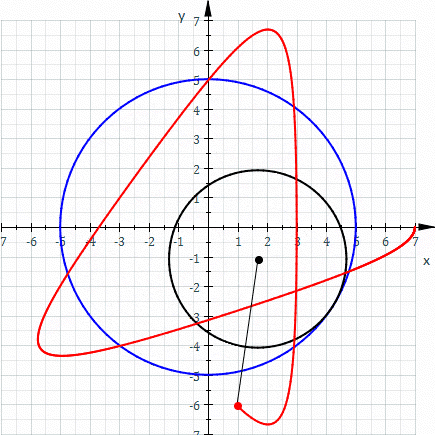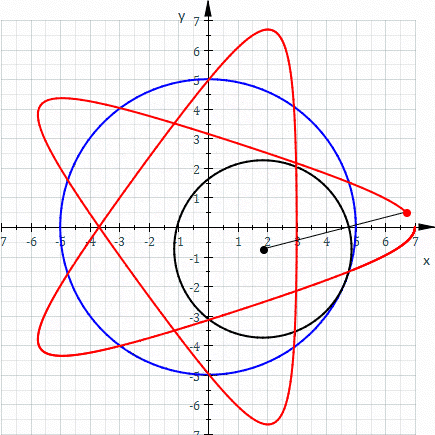
A spirograph is made by rolling a circle around another circle, like thiis:

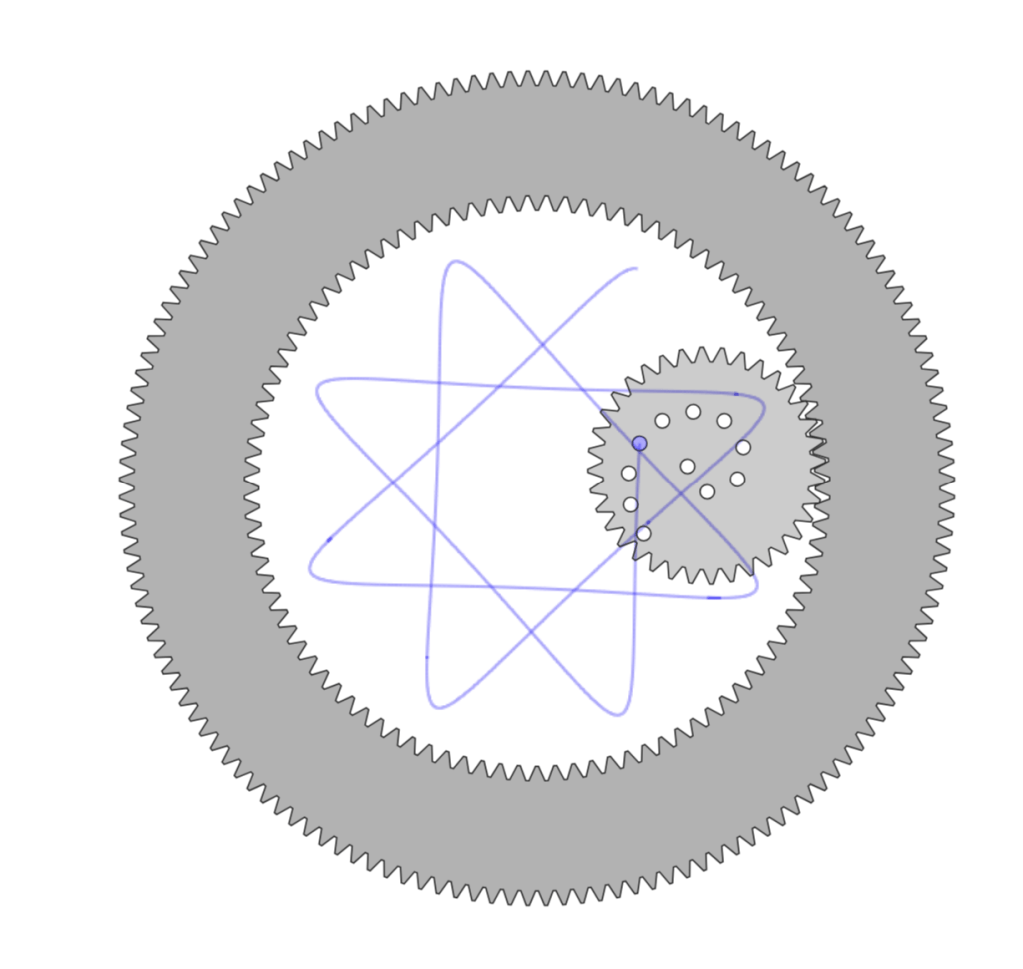
There are two basic types of spirographs: an epitrochoid and a hypotrochoid.

An epitrochoid is made like this:

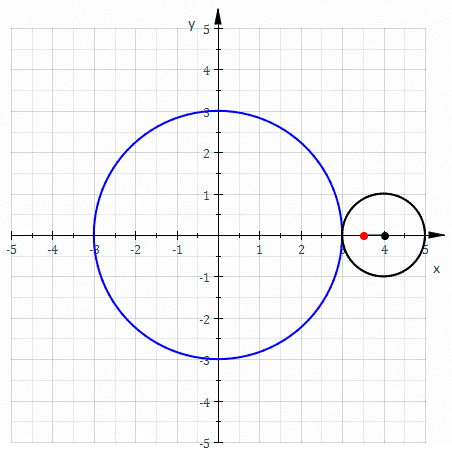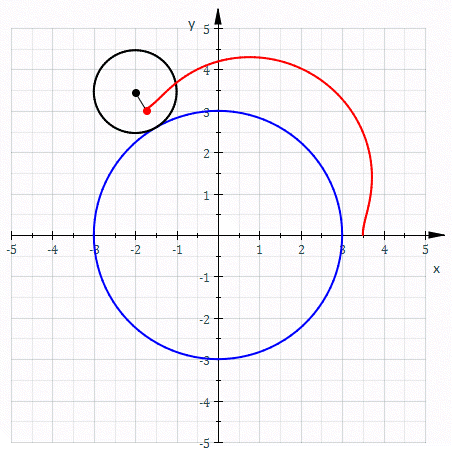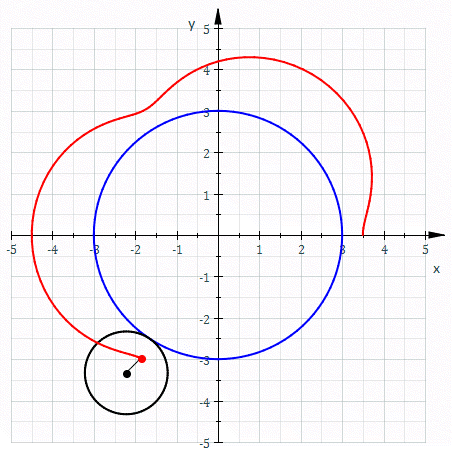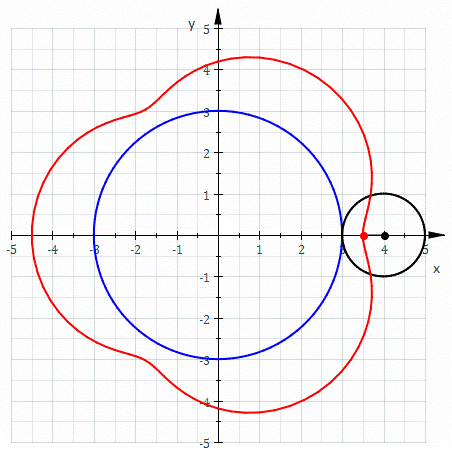
A hypotrochoid is made like this:

The equation of a spirograph

The equation for an epitrochoid is:

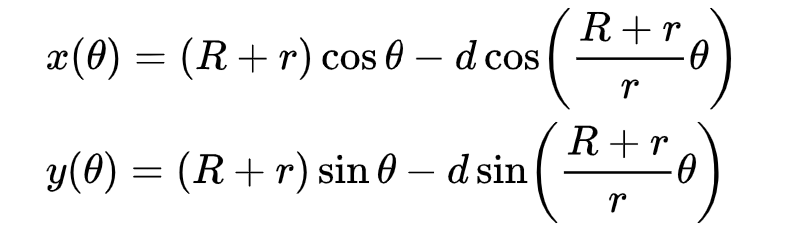
The equation for a hypotrochoid is:

You can see that the two sets of equations are very similar. They will look even more similar if we set a variable, m = R + r, or R – r, respectively.

In each case:

  • R represents the radius of the stationary circle
  • r represents the radius of the moving circle
  • d represents the distance from the center of the moving circle to the pen

In the case of an actual, physical Spirograph, d is always less than r.

Special situations

For a hypotrochoid, when d = r, it becomes a hypocycloid. For an epitrochoid, when d = r, it becomes an epicycloid. In both of these cases, the pen is sitting on the circumference of the circle.

When d = 0, both a hypotrochoid and an epitrochoid become a circle.

When the moving circle is the same diameter as the fixed circle, R = r, they become a special curve called a limacon.

Patterns

The curves are always symmetric about the x-axis, and they are symmetric about the y-axis when m/r is odd.

If m/r is an integer, then there will be m/r – 1 loops.

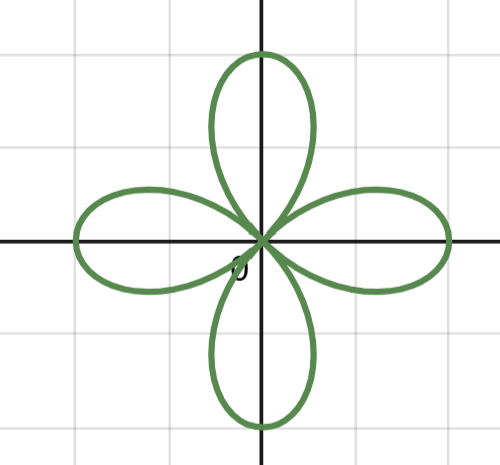
Hypotrochoid with R = 4, r = 3, d = 1

R = 6, r = 2.4, d = 1

Website

The following website lets you draw spirographs:

Inspiral Web (nathanfriend.io)

Desmos

These curves can be drawn on Desmos in the form of (x(t), y(t)), like this:

Other curves

There are dozens of other interesting curves, which can be found at these websites:

Coming up…

This is the first of a multi-part series on spirographs. Be sure to read the next post in this series.

Comments

Leave a comment