CoMo Science

Spirographs 2

—

in , ,

This is part 2 of a multi-part series. If you haven’t read the first part, it may be helpful to review it first.

  1. The problem with the standard formulas
  2. A change of variables
  3. Desmos
  4. Coming up…

The problem with the standard formulas

The standard formula for an epitrochoid is:

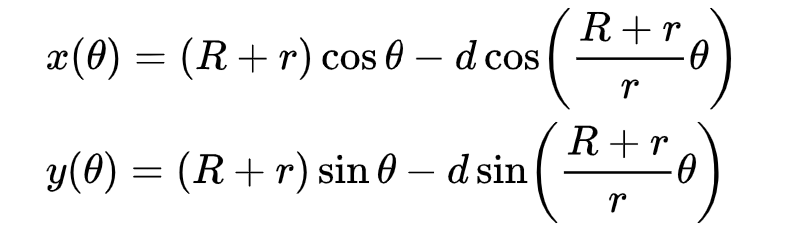
The problem with this formula is that adjusting r or d to form new designs changes the overall size of the design. The radius of the design is equal to the sum of the radius of the large circle, the radius of the small circle and d.

This can be a problem when creating a pattern for 3D printing or laser etching.

There is, of course, a similar problem with the formula for the hypotrochoid.

A change of variables

It would be nice to have 3 parameters which can be individually adjusted. The parameters we would want to adjust would be the:

  • overall size of the design
  • how many lobes the design has, which is determined by the ratio of the radii of the circles
  • how “loopy” the design is, which is determined by the ratio of d to the radius of the moving circle

This gives us a system of three equations:

  • A = R + r + d
  • B = R/r
  • C = d/r

Substituting the second and third equations into the first equation gives:

A = B*r + r + C*r = r*(B + 1 + C)

Therefore, r = A/(B+C+1)

Plugging this into the second and third equations gives R = A*B/(B+C+1) and d = A*C/(B+C+1)

Substituting these new variables into the epitrochoid formula gives:

x = (AB + A)/(B+C+1)·cos(θ) – AC/(B+C+1)·cos((B-1)·θ)

y = (AB + A)/(B+C+1)·sin(θ) – AC/(B+C+1)·sin((B-1)θ)

Desmos

Here is the related hypotrochoid formula entered in Desmos:

Now, adjusting A increases or decreases the size of the design

Adjusting B adjusts the number of lobes. Specifically, integer values give a finite number of lobes.

Adjusting C changes the size of the loops.

Below is the formula arranged as an (x,y) pair that can be copied and pasted directly into Desmos:

((AB-A)/(B+C-1)cos(t)+AC/(B+C-1)cos((B-1)t),(AB-A)/(B+C-1)sin(t)-AC/(B+C-1)sin((B-1)t))

Coming up…

The next post in this series discusses using this formula to write a Python program to generate G-code to control a 3D printer or laser cutter to make spirographs.

Comments

Leave a comment