8/29/24

Greek and Latin Roots

Here is the list of Greek and Latin roots for this week:

Roots chart Download

Here is a link to all of the Greek and Latin roots we have discussed.

Greek and Latin Roots

Test your memory of the Greek and Latin roots that we have discussed with this quiz.

This is the link to the Wikipedia list of Greek and Latin roots.

ACT Prep

The equation to find a percent is:

Percent = Percentage x Whole

To find 19% of 310, 58.9 = .19 x 310

Numbers can be rounded to quickly estimate the answer and eliminate some possibilities.

.2 x 300 = 60

There are three types of means you should know: mean, median and mode, as well as the range.

Presentations

The goal of the presentations is to:

Motivate you to be curious and pursue an interesting topic that you haven’t been taught in school.
Practice present the topic and explaining it to others
Introduce others to the topic
Help you with parts of the concept that you didn’t fully understand

Assignments

Fill out the list of Greek and Latin roots.
- Write in the meaning of each root
- Give at least one example of each, be prepared to give its actual definition and the way that it is related to the root word
  - Example: If I gave you the root “onym”, you could give the word “synonym” which has the definition of two words with the same meaning. The two roots in the word “syn” and “onym” mean “same name”, indicating two words that name the same thing.
- Fill out the blank space at the bottom with your own root that you have discovered. This will likely come from some of the example words that you have already written. Give a different example than what you have used.
  - Example: syn- means “same”, example word “synchronous”
- Be prepared to talk about where you found this information.
Presentation
- Research your topic of choice and be prepared to give a 5 minute presentation on the topic, geared toward people your age level.
- Include the background information needed for someone who does not know the topic as well as you.
- Be prepared to talk about how you found this information.

Things We Discussed

Greek and Latin roots

Hemiplegia

Hemiplegia is loss of function of have of your body. This is usually either one side of your body (from a brain injury, like a stroke) or the lower half of your body (from injury to your spinal cord). If a spinal cord injury occurs higher (like in your neck), you can lose control of all four limbs. This is called quadriplegia.

This is a picture of the dermatomes, which are the regions of the skin innervated by the spinal nerves coming from each level of the spinal cord. A similar picture, called the myotomes, shows the muscles controlled by each nerve.

This allows you to see where the injury in the spinal cord would need to be to cause hemiplegia or quadriplegia.

Euler’s formula

There are many fundamental math concepts that need to be understood to understand Euler’s formula. These include imaginary numbers, trigonometric functions, radians, and Taylor series.

Complex numbers

The degree of a polynomial is determined by its highest power. For instance, a quadratic equation, such as y = x² + 5x + 3, has a degree of two.

The fundamental theorem of algebra says that a polynomial equation of nth degree will always cross the line y=0 exactly n times. For instance, the equation y = mx + b (a line) is a first order equation and crosses once. The equation y = x² – 1 is a parabola that crosses the line y = 0 two times.

The values of x where the equation crosses the line y = 0 are called roots. Roots are found by solving the equation for x when y = 0.

However, the equation x² + 1 does not seem to cross the line y = 0. In other words, it does not seem to have any roots. If x² + 1 = 0, then x² = -1. But there is no real number that can be squared to get -1.

In order to satisfy the fundamental theorem of algebra, mathematicians eventually had to accept that there is a number that satisfies this equation, which they called i.

Starting with this, you can see there are an infinite number of imaginary numbers by multiplying i by any real number.

When a real number, a, and an imaginary number, bi are added together, they form a complex number, a + bi. This can be graphed on the complex plane.

This is a great video about complex numbers:

Trigonometric functions

The ratios of the sides of a triangle are determined by the angles of the triangle. No matter how big the triangle is, the ratios will be the same.

We can use this fact to define certain, very important, functions.

The sine of an angle is the opposite side/hypotenuse. This is written as sin(θ) or sin θ.

The cosine of an angle is the adjacent side/hypotenuse. This is written as cos(θ) or cos θ.

There are several other functions, but these are the two most important.

The sine of 0 degrees is 0 because the opposite side has no height.

The cosine of 0 degrees is 1 because the length of the adjacent side is equal to the length of the hypotenuse.

The sine and cosine can be extended to include angles greater than 90.

In turns out that the sine of 180 degrees is also 0, and the cosine of 180 degrees is -1.

Radians

Degrees is an arbitrary measure of an angle, used simply because 360 is easily divided by 1,2,3,4,5,6, and so on.

There is another measure of an angle called a radian. A radian is defined as the angle where the arc of the circle subtended by the angle has the same length as the radius of that circle.

Radians are often used in trigonometry and always used in calculus.

Degrees can be converted to radians and back based on the fact that there are 360 degrees in a circle and 2π radians (since the arc length of a complete circle is its circumference which equals 2πr).

Calculus

There are two major concepts in calculus:

The derivative – which is a way to calculate the slope of a curve at any point

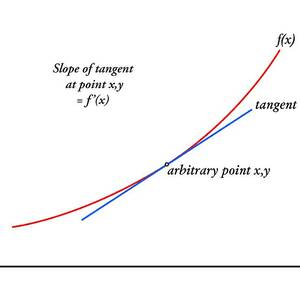
The integral – which calculates the area under a curve

There are many ways that these two concepts can be put to use.

For instance, the slope of a curve is zero at any point where there is a local maximum or minimum.

But, not only that, you can also take the derivative of the derivative (called the second derivative), to determine whether the point is a maximum or a minimum (or neither, called an inflection point).

Taylor series

The first derivative, second derivative and as on, each give additional information about how the curve behaves at a point.

This fact can be used to develop a formula for any function based on the derivatives of the function. This is called a Taylor series. It is called a series because the formula is an infinite series of terms all added together.

Here are some common Taylor series:

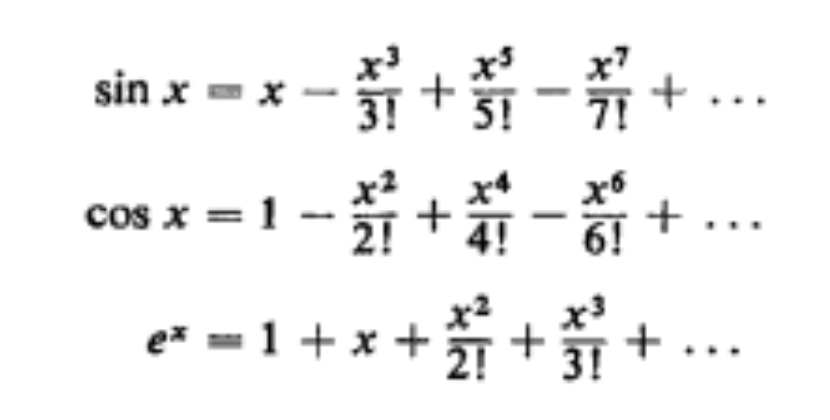
You can see that the terms in sin x and cos x add up to e^x, except that half of the cosine terms are negative. However, when i is raised to powers of 2, 6, 10, etc., it equals -1, which cancels out the negative sign.

Euler’s formula

When the Taylor series for cos(x) and i·sin(x) are added together, it gives the Taylor series for e^ix.

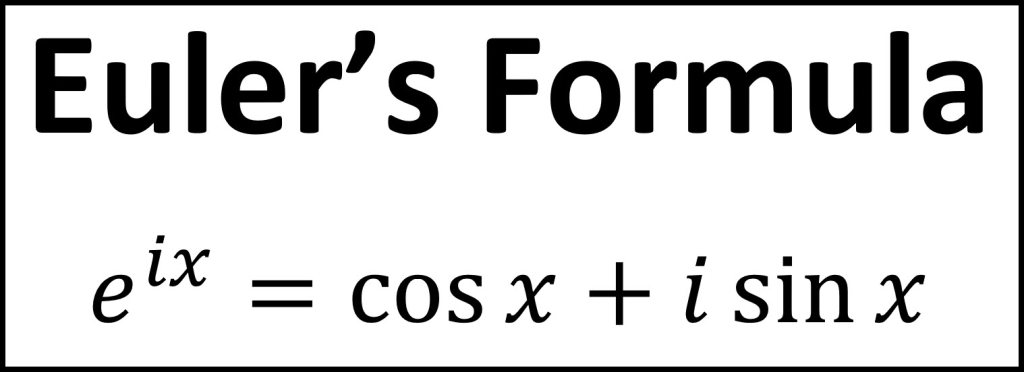
In the case of x = π, cos(π) = -1 and the sin(π) = 0, since π radians is the same as 180°, and, as discussed above, cos(180°) = -1 and sin(180°) = 0.

This gives:

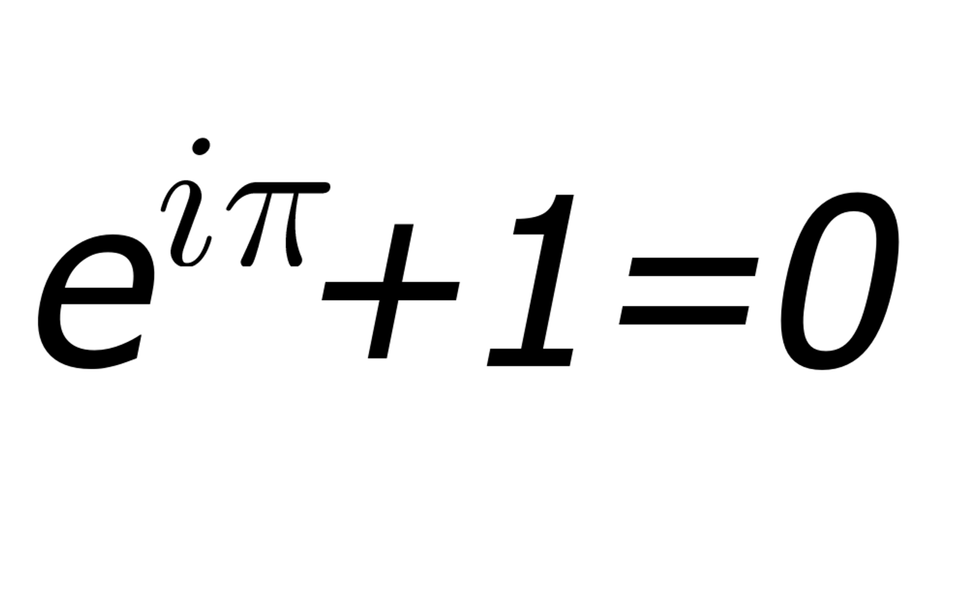
Averages

There are three averages that are commonly taught in pre-algebra: the mean, median and mode.

The mean is properly known as the arithmetic mean because there are actually many different means.

Two additional means which you may sometimes come across are the geometric mean and the harmonic mean.

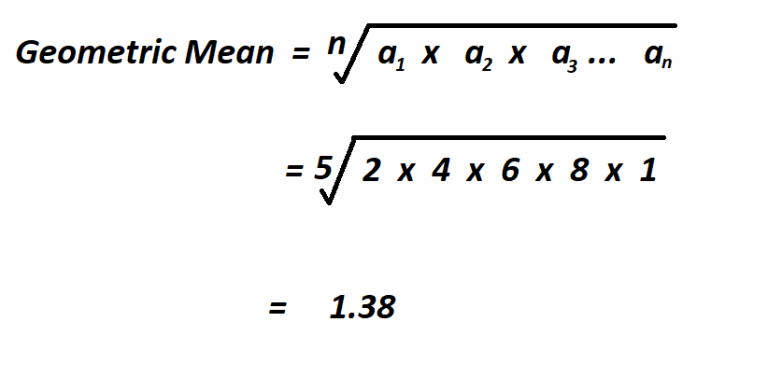
Bimodal

Some graphs have two distinct peaks. Even though one peak is almost always higher than the other (and is the true mode), sometimes the second peak is so prominent that the graph is referred to as “bimodal”.

As you can see, a bimodal distribution often occurs because two different processes (in this case, the blue and red curves) overlap, adding together to produce one curve with two peaks.

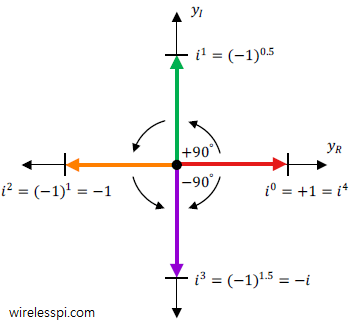
Complex numbers and rotations

Multiplying by i leads to a rotation. This can be seen when the powers of i are graphed.

power of i	result
i⁰	1
i¹	i
i²	-1
i³	–i
i⁴	1

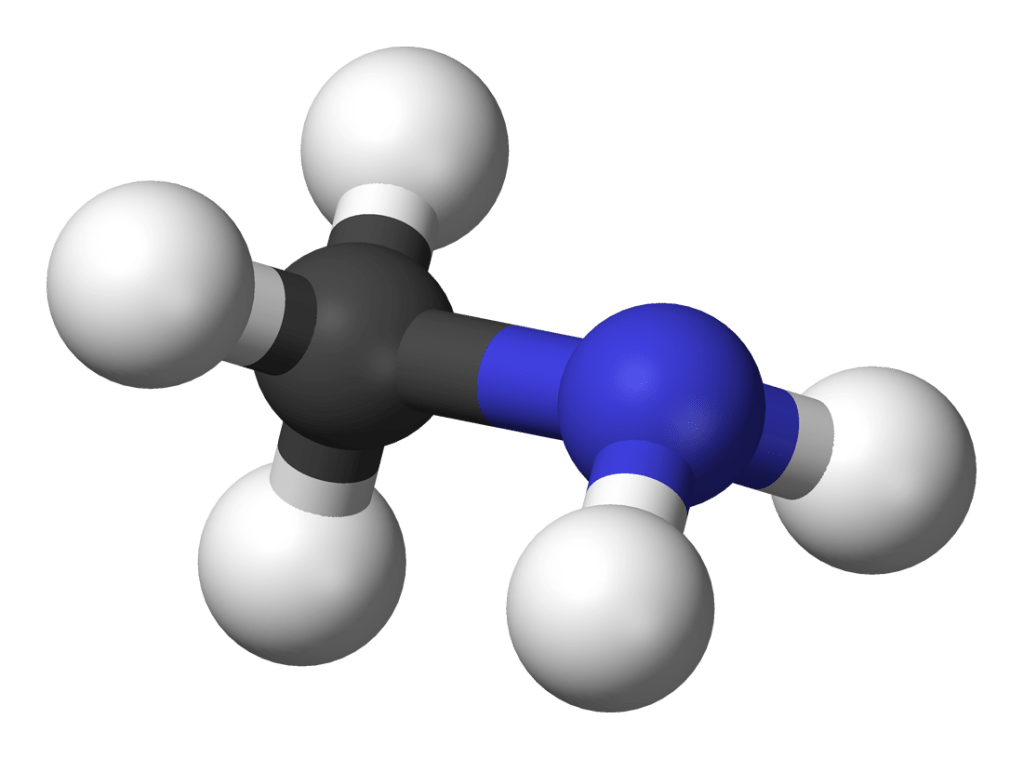
Methylamine

This molecule has a methane combined with ammonia and therefore has a methyl group and an amino group. It is known as methylamine (not aminomethane). It has the smell of rotting fish, which is common among small amine molecules.

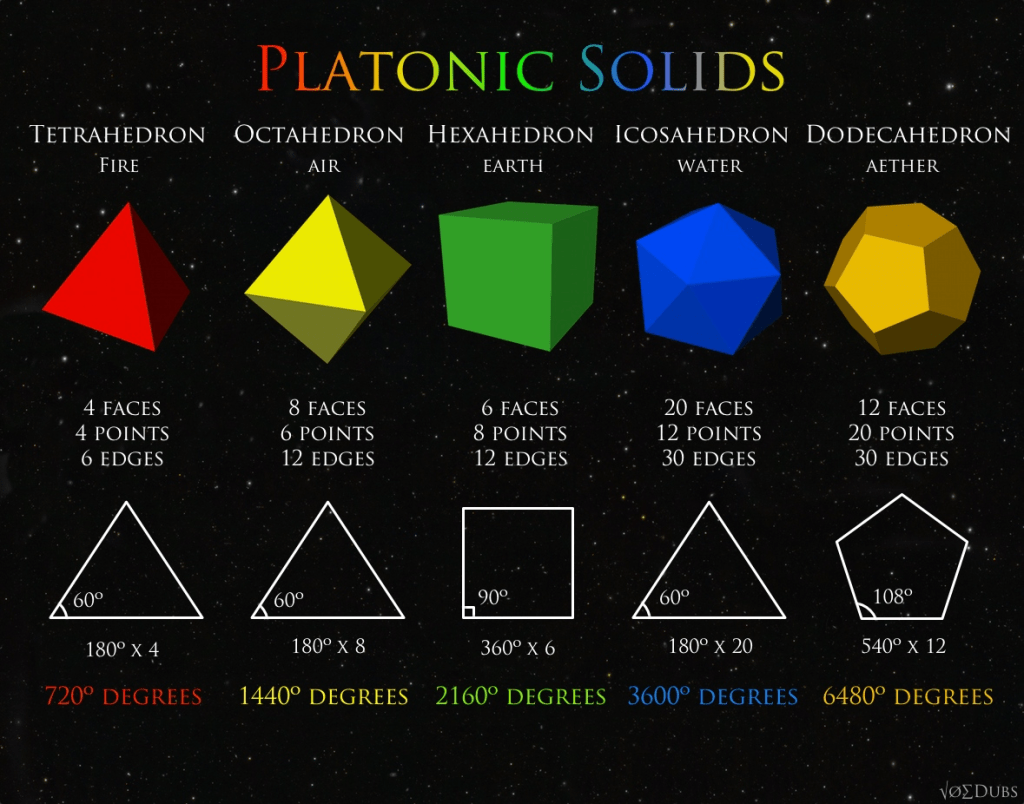
Tetrahedrons

A tetrahedron is a four-sided object that is shaped like a pyramid. It is one of the Platonic solids, the others being a cube, octahedron, duodecahedron, and the icosahedron.

Methane molecules have a tetrahedral structure.

Igneous, metamorphic and sedimentary rocks

Rocks can be classified into 3 groups based on the way they were formed:

Type	Formed by
igneous	cooling of molten rock (lava or magma)
sedimentary	compression of small particles of eroded rock
metamorphic	secondary changes to igneous or sedimentary rock from high heat and pressure

The rock cycle shows how these types of rocks can be changed into each other:

Types of metamorphic rocks

gneiss, pronounced “nice”, a metamorphic rock, started as granite, an igneous rock. Gneiss feels and acts much like granite, however, you can see from the folded layers in it that it has undergone metamorphosis.

Slate is a metamorphic rock that started as shale, a sedimentary rock.

You typically won’t find fossils in igneous or metamorphic rock because of the way that it is formed. However, the village of Pompeii demonstrates a way that fossils can form from a volcanic eruption.

Programming

The following are programs that print the numbers from 1 to 10 on the computer screen.

void main() {
     for (int i = 1; i<=10; i++) {
          printf("%d\n",i);
     }
}

Python:

for i in range(1,11):
     print(i)

In both programs, the procedure that is being followed to produce the output is the same. As you can see, C requires a lot more punctuation. The syntax of Python is simpler. This makes Python simpler to learn and easier to debug.

There are some benefits to using C. For one, C is a compiled language which makes the program run much faster. In contrast, Python is an interpreted language which is generally slower.

8/29/24

Greek and Latin Roots

ACT Prep

Presentations

Assignments