There are many fundamental math concepts that need to be understood to understand Euler’s formula. These include imaginary numbers, trigonometric functions, radians, and Taylor series.

Complex numbers

The degree of a polynomial is determined by its highest power. For instance, a quadratic equation, such as y = x² + 5x + 3, has a degree of two.

The fundamental theorem of algebra says that a polynomial equation of nth degree will always cross the line y=0 exactly n times. For instance, the equation y = mx + b (a line) is a first order equation and crosses once. The equation y = x² – 1 is a parabola that crosses the line y = 0 two times.

The values of x where the equation crosses the line y = 0 are called roots. Roots are found by solving the equation for x when y = 0.

However, the equation x² + 1 does not seem to cross the line y = 0. In other words, it does not seem to have any roots. If x² + 1 = 0, then x² = -1. But there is no real number that can be squared to get -1.

In order to satisfy the fundamental theorem of algebra, mathematicians eventually had to accept that there is a number that satisfies this equation, which they called i.

Starting with this, you can see there are an infinite number of imaginary numbers by multiplying i by any real number.

When a real number, a, and an imaginary number, bi are added together, they form a complex number, a + bi. This can be graphed on the complex plane.

This is a great video about complex numbers:

Trigonometric functions

The ratios of the sides of a triangle are determined by the angles of the triangle. No matter how big the triangle is, the ratios will be the same.

We can use this fact to define certain, very important, functions.

• The sine of an angle is the opposite side/hypotenuse. This is written as sin(θ) or sin θ.

• The cosine of an angle is the adjacent side/hypotenuse. This is written as cos(θ) or cos θ.

There are several other functions, but these are the two most important.

The sine of 0 degrees is 0 because the opposite side has no height.

The cosine of 0 degrees is 1 because the length of the adjacent side is equal to the length of the hypotenuse.

The sine and cosine can be extended to include angles greater than 90.

In turns out that the sine of 180 degrees is also 0, and the cosine of 180 degrees is -1.

Radians

Degrees is an arbitrary measure of an angle, used simply because 360 is easily divided by 1,2,3,4,5,6, and so on.

There is another measure of an angle called a radian. A radian is defined as the angle where the arc of the circle subtended by the angle has the same length as the radius of that circle.

Radians are often used in trigonometry and always used in calculus.

Degrees can be converted to radians and back based on the fact that there are 360 degrees in a circle and 2π radians (since the arc length of a complete circle is its circumference which equals 2πr).

Calculus

There are two major concepts in calculus:

• The derivative – which is a way to calculate the slope of a curve at any point

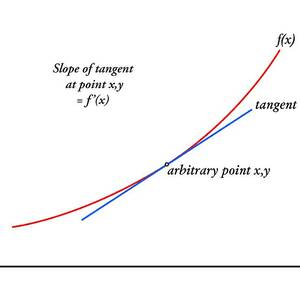
• The integral – which calculates the area under a curve

There are many ways that these two concepts can be put to use.

For instance, the slope of a curve is zero at any point where there is a local maximum or minimum.

But, not only that, you can also take the derivative of the derivative (called the second derivative), to determine whether the point is a maximum or a minimum (or neither, called an inflection point).

Taylor series

The first derivative, second derivative and as on, each give additional information about how the curve behaves at a point.

This fact can be used to develop a formula for any function based on the derivatives of the function. This is called a Taylor series. It is called a series because the formula is an infinite series of terms all added together.

Here are some common Taylor series:

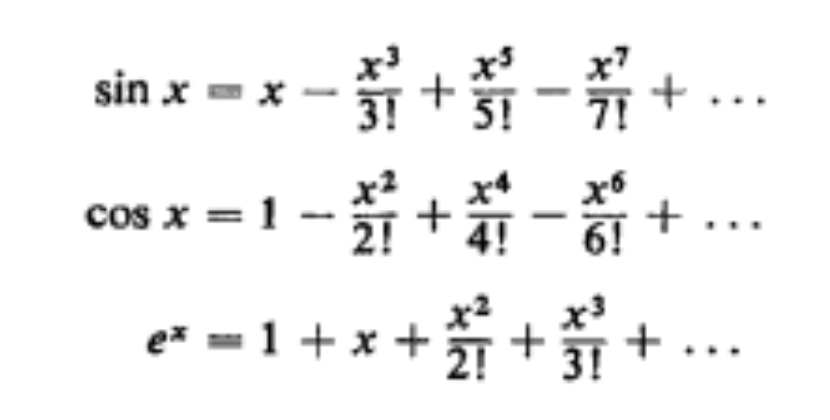
You can see that the terms in sin x and cos x add up to e^x, except that half of the cosine terms are negative. However, when i is raised to powers of 2, 6, 10, etc., it equals -1, which cancels out the negative sign. In the same way, the odd powers of i give either i or –i, which is why the sin x is multiplied by i in the equation below.

Euler’s formula

When the Taylor series for cos(x) and i·sin(x) are added together, it gives the Taylor series for e^ix.

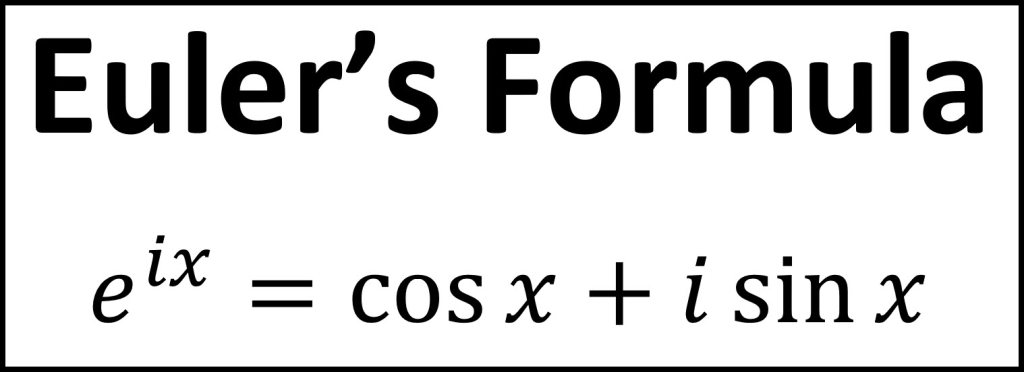
In the case of x = π, cos(π) = -1 and the sin(π) = 0, since π radians is the same as 180°, and, as discussed above, cos(180°) = -1 and sin(180°) = 0.

This gives the Euler identity:

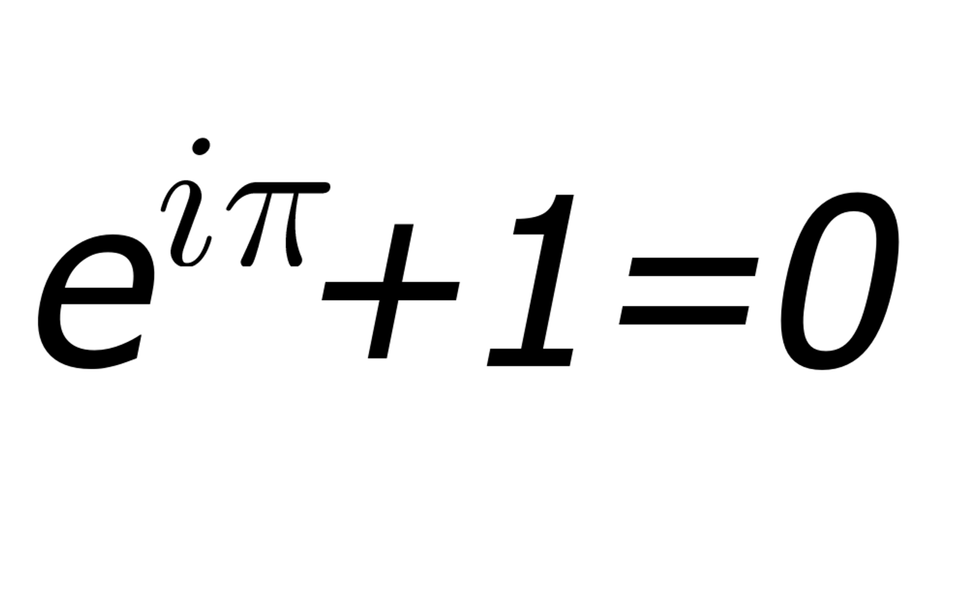
This is considered one of the most beautiful equations in mathematics. It combines 5 basic mathematical constants.