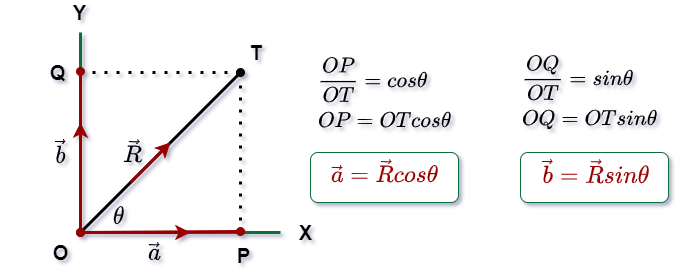
What do X and Y represent?
X and Y are indicating the x- and y-axes.
What does the arrow above the a, b, and R represent?
The arrow indicates that a, b, and R are vectors.
What does θ represent?
θ is the lowercase Greek letter theta which is often used to represent an angle.
Other Greek letters that are often used to represent angles include alpha (α), beta (β), gamma (γ) and phi (φ).
What are O, Q, T, and P?
They are points.
What are OP, OT, and OQ?
They are the lengths of the line segments. If you said they represent the line segments themselves, you would be close but technically incorrect. There should be a line segment drawn over OP, for example, to represent the line segment OP. Without the line segment, it is the distance between O and P. This is consistent with the fractions, since you cannot divide one line segment by another one. You can only divide their distances.
What does cos represent?
“cos” is short for cosine, a function that is defined as the ratio of the lengths of the adjacent side divided by the hypotenuse. In this case, as the equation shows, the side adjacent to the angle θ is the line segment OP, and the hypotenuse is the line segment OT.
What does sin represent?
“sin” is short for sine, a function that is defined as the ratio of the lengths of the opposite side divided by the hypotenuse. In this case, the side opposite to the angle θ is the line segment PT. This is NOT what the equation shows. However, the equation is still correct because the length of the line segments OQ and PT are the same.
What lengths are the same in this diagram?
OP = QT
OQ = PT
OP looks like the same length as OQ, but this diagram is meant to be general and should not be assumed to be to scale.
What do the dotted lines represent?
They represent where you could move either vector a or vector b (but not both at the same time) to add vectors a and b together to get vector R.
They can also be interpreted to mean that the y coordinate of T is the same as Q and the x coordinate of T is the same as P.
Which angle can be interpreted as being the same as θ?
It is reasonable to expect that the dotted lines are parallel to their projections on the axes.
This makes OT a transversal. By the transverse angle theorem, corresponding angles are equal. Therefore, angle QTO is congruent to TOP.
What would θ be if OQ = OP?
45°
How are the red equations different from the equations directly above them?
OP and OT are numbers (the lengths of the line segments). Vectors a and R are vectors. Vectors have both a length (called its magnitude) and a direction. OP is the same as PO; they are the same length. Line segment OP is the same as line segment PO; they are both the same line segment. However, the vector from OP is not the same as the vector from PO because they have different directions.
In the red equations, a and R are vectors. What is cos θ called?
cos θ is a number. A number has only a magnitude but no direction. A number is called a scalar.
What is one physical quantity that is a scalar and one that is a vector?
Examples of scalar quantities:
- mass
- temperature
- length
- speed
- energy
Examples of vector quantities:
- force
- acceleration
- velocity
- momentum
What is wrong with this diagram?
The arrows should be at the end of the vectors with the tips touching the end points Q, T and P.
Leave a comment